引言

自己动手写分布式KV存储引擎系列文章的目标是记录基于LevelDB(RockDB)构建一个分布式KV存储引擎实现过程，此系列文章对应的源码在DSTORE。

本文主要分析了网络框架中定时器的原理及实现，全文分为如下两部分

定时器的功能设计
定时器的功能实现

本系列的其他文章还包括：

自己动手写分布式KV存储引擎（一）：设计和实现网络框架

定时器的功能设计

本节主要分析了服务端程序对定时器的需求，定时器的算法选择。

需求

在服务端编程中，很多地方会使用到定时器，例如：

服务端定时发送心跳，证明自身在线
服务器检测到某些连接在一定时间内不活跃后，可以关闭其连接

这些功能都是使用频率非常高的功能，其性能的好坏与定时器本身的性能好坏密不可分，因此，实现一个高性能的定时器是非常有必要的。接下来分析影响定时器性能最重要的因素：定时器的算法选择。

定时器算法选择

在一个网络框架中，对定时器的操作主要包括：

插入定时器，记做INSERT
更新定时器的超时时间，维持定时器超时时间按照从小到大的顺序，记做UPDATE
按照超时时间获取下一个定时器，记做GET
删除定时器，记做DELETE

以维持心跳功能为例，讨论定时器功能采用何种算法才能获得高性能。

一个典型的连接之间维持心跳的事件发生序列如下：

建立连接，设置定时器，并注册到网络框架中，即INSERT操作
网络框架在定时器到期时，需要从其维护的定时器池中取出来，调用相应的处理接口，然后，更新定时器的超时时间，维持定时器池中按照定时器超时时间，即GET+UPDATE操作
在链接关闭前，重复步骤2多次，记做次数为K
关闭连接，记做DELETE操作

即从连接开始到连接关闭，整个发生的定时器事件为1 INSERT + K GET + K UPDATE + 1 DELETE。

算法选择

普通链表

INSERT：插入到链表尾部，算法时间复杂度O(1)
UPDATE：就地更新，算法时间复杂度O(1)
GET : 需要遍历链表，获取超时时间最小的定时器，算法事件复杂度O(N)
DELETE : 采用双向链表的话，删除任意一个节点的时间复杂度为O(1)

因此，采用普通链表，上述事件整体时间复杂度为O(1) + K * O(N) + K * O(1) + O(1)，即K * O(N)

有序链表

INSERT : 插入到链表合适位置，保持有序性质，算法时间复杂度为O(N)
UPDATE : 更新超时时间后，需要把其插入到链表合适位置，保持有序性质，算法时间复杂度为O(N)
GET : 获取下一个超时时间最小的定时器，由于是排序链表，算法事件复杂度为O(1)
DELETE : 采用双向链表的话，删除任意一个节点的时间复杂度为O(1)

因此，采用排序链表，上述事件整体时间复杂度为O(N) + K * O(N) + K * O(1) + O(1)，即(K+1) * O(N)

堆

INSERT : 插入一个元素入堆，保持堆的性质，算法时间复杂度为O(lgN)
UPDATE : 更新超时时间后，需要维持堆的性质，算法时间复杂度为O(lgN)
GET : 由于每次更新和插入都保持了堆的性质，因此，此操作算法时间复杂度为O(1)
DELETE : 删除元素后，也需要保持堆的性质，算法时间复杂度为O(lgN)

因此，采用堆，上述事件整体时间复杂度为O(lgN) + K * O(1) + K * O(lgN) + O(lgN)，即(K+2) * O(lgN)。

排序树

INSERT : 插入一个元素，保持排序树的性质，算法时间复杂度为O(lgN)
UPDATE : 更新超时事件后，需要维持排序树的性质，算法时间复杂度为O(lgN)
GET : 需要找到最左叶子节点，算法时间复杂度为O(lgN)
DELETE : 删除元素后，也需要保持排序树的性质，算法时间复杂度为O(lgN)

因此，采用排序树，上述整体时间复杂度为O(lgN) + K * O(lgN) + K * O(lgN) + O(lgn)，即(2K+2) * O(lgN)。因为普通的排序树可能会导致不平衡，使得时间复杂度恶化到O(N)，因此，上述分析假定采用的是平衡树的方法，对于平衡树，其更新等操作的对应时间复杂度的常量因子往往是大于堆的。

考虑上述算法的时间复杂度，可以看出采用堆的算法时间复杂度最小，因此，本文中的定时器采用堆来实现。

定时器的功能实现

由于采用堆实现定时器，先来描述一下堆的实现原理。

堆原理

堆分为大根堆和小根堆，由于本文中的定时器按照超时时间升序排列，所以，以小根堆为例描述堆的基本原理。

首先来看堆的定义，引用自维基百科-堆

n个元素序列{k1,k2…ki…kn},当且仅当满足下列关系时称之为堆：
(ki <= k2i,ki <= k2i+1)或者(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4…n/2)

前面括号中描述的即小根堆，即把堆看成一棵二叉树，则小根堆保证父节点的值要小于或等于子节点的值。

堆有以下特性：

任意节点小于（或大于）它的所有子节点，最小元（或最大元）在堆的根上（堆序性）。
堆总是一棵完全树。即除了最底层，其他层的节点都被元素填满，且最底层尽可能地从左到右填入

一般地，在堆上支持以下几种操作：

build：将数组构造成堆
insert：向堆中插入一个元素
update：更新堆元素的值
get：获取堆顶元素的值
delete：删除堆中任意元素

上述的操作都依赖于堆调整操作，分为向下调整和向上调整，调整的目的是为了在所调整的树路径上，维持堆的性质。

向下调整

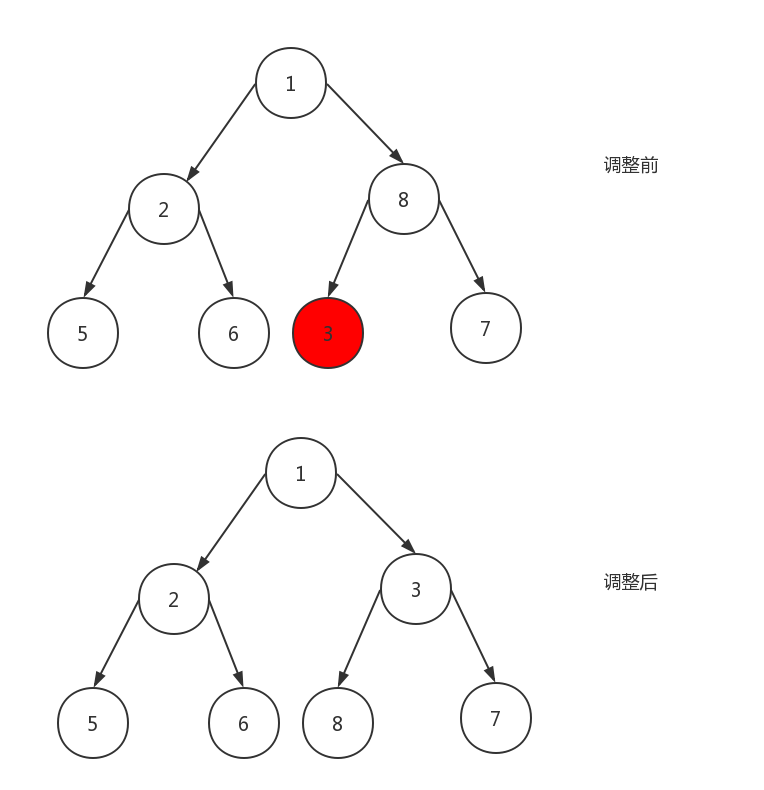
如上图所示，从节点值为8的节点开始调整，首先，找出8的子节点中，较小者，即3。然后，如果较小的子节点(3)，小于父节点(8)，那么，则将父子节点交换。最后，再从交换后的节点开始，直到到达叶子节点或者父节点比两个子节点都大。

向上调整

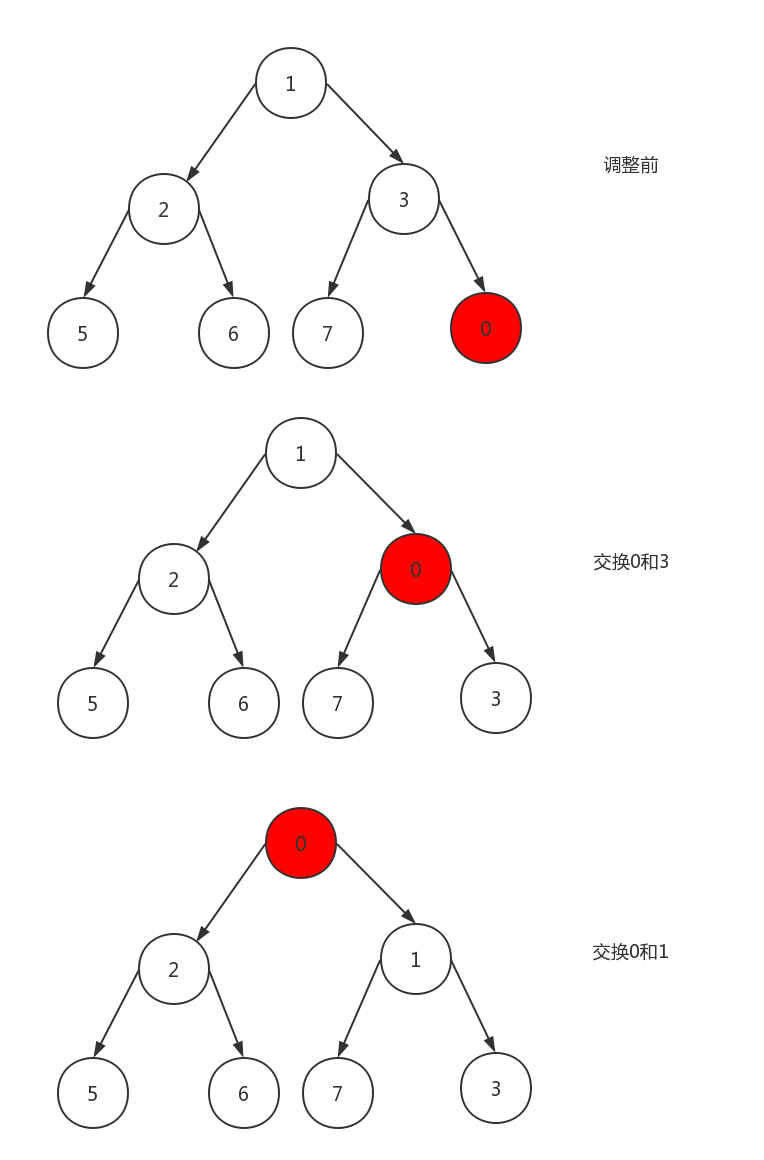
如上图所示，从节点0开始调整，如果其父节点大于它，则互相交换，即途中的交换0和3；继续在交换后的位置开始，节点0和父节点1比较，父节点1大于子节点0，因此，继续交换，最终，得到调整后的堆。

堆支持的几种操作都能通过上述的向上调整和向下调整来实现。

build

因为堆是一棵完全树，所以，一般采用数组的方式来实现它。假设数组为array，其长度为n，节点下标为(0…n-1)

从最后一个非叶子节点开始采用向下调整的方法，保证其下的子树维持堆性质；然后不断地循环此过程，直到达到下标为0的节点。

1
2
3

for (int i = n/2; i >=　0; i--) {
	down_heap(array, i, n);
}

insert

把插入的元素放到数组最后，这样，它的插入可能会引起其所在父节点不满足堆性质，进行相应的调整，这和向上调整的过程是一致的，即

1 2	array.push_back(element); up_heap(array, element_index);

update

更新堆元素的值，分为两种情况：

第一种是更新后，使得其比父节点小，那么，需要采用向上调整
第二种是更新后，使得其比子节点中的某个小，那么，需要采用向下调整

array[update_index] = new_value;
if (array[update_index] < array[update_paraent_index]) {
	up_heap(array, update_index);
} else {
	down_heap(array, update_index, array.size());
}

get

由堆的性质可以得出，堆顶元素是最小的，因此，只要返回数组的第一个元素。

1	return array[0];

delete

可以把该元素对应的值改成最小，然后，根据堆的特性，调整后其会到堆顶，然后，再将堆顶的元素和堆最末元素交换，重新调整堆。

array[update_index] = -1;
up_heap(array, update_index);
swap(array, 0, array.size()-1);
down_heap(array, 0, array.size()-1);

定时器实现

定时器支持的功能如下：

插入定时器
删除定时器
获取所有超时的定时器
更新定时器的超时时间

在实现定时器时，首先想到的是采用STL提供的接口，但查看文档后发现STL只支持从堆顶删除元素，不支持从堆的中间删除元素，因此，本文的定时器是在std::vector基础上，自己实现的堆。

插入定时器

首先，先把定时器放到数组最末，然后，采用向上调整的方法使得堆性质保持，伪代码如下

void EventLoop::push_timer_heap(Event *e) 
{                   
  e->index = timer_heap_.size();
  e->timeout += get_milliseconds();
  timer_heap_.push_back(e);
  adjust_timer_heap(e->index, timer_heap_.size(), timer_heap_);
}

删除定时器

把相应的定时器的超时时间改成负数，然后采用向上调整的方法，把该定时器调整到堆顶；然后，交换堆顶和堆尾元素，再采用向下调整的方法调整第一个元素到倒数第二个元素之间的序列，使其维持堆性质，最后，删除掉最后一个元素，伪代码如下

void EventLoop::pop_timer_heap(void)
{                
  swap_timer_event(0, timer_heap_.size() - 1);
  adjust_timer_heap(0, timer_heap_.size() - 1, timer_heap_);
  timer_heap_.pop_back();
}                          
void EventLoop::remove_timer_heap(const Event *e)
{                
  timer_heap_[e->index]->timeout = -1;
  adjust_timer_heap(e->index, timer_heap_.size(), timer_heap_);
  pop_timer_heap();
}

获取所有超时的定时器

从堆顶获取元素，比较超时值和当前时间的关系，分为两种情况：

如果超时值小于或等于当前时间，那么，说明定时器已经超时，调用它的处理函数，然后，采用pop_timer_heap将其弹出，并继续比较超时时间与当前时间的关系，如果满足小于或等于，则重复步骤1，否则跳转到步骤2
如果超时值大于当前时间，那么，说明最小的定时器超时时间还未到，则退出处理

伪代码如下

void EventLoop::process_timeout_events(void)
{ 
  const int64_t now = get_milliseconds();
  Event *e = top_timer_heap();
  while (e != nullptr && e->timeout <= now) {
    e->timer_cb(e->fd, Event::kEventTimer, e->args);
    pop_timer_heap();
    e = top_timer_heap();
  }
}

更新定时器超时时间

更新定时器的超时时间，分为两种情况：

如果更新的值小于其父节点的值，那么采用向上调整
如果更新的值大于其父节点的值，那么采用向下调整

为了能用定时器直接获得对应的堆数组的下标，每个定时器事件中都保存了其在堆数组的下标，避免了为了查询堆数组下标而需要遍历数组而带来的性能开销，伪代码如下

void EventLoop::process_timeout_events(void)
{ 
  const int64_t now = get_milliseconds();
  Event *e = top_timer_heap();
  while (e != nullptr && e->timeout <= now) {
    e->timer_cb(e->fd, Event::kEventTimer, e->args);
    pop_timer_heap();
    e = top_timer_heap();
  }
}

上述所有的操作都是基于二叉堆来实现的，从堆的操作来看，其在数组中操作的元素相隔较远(父子节点的下标都是2倍关系)，因此，二叉堆对cache并不友好。在libev中采用四叉堆来缓解上述问题，据其代码中描述，四叉堆在5w+的定时器下，能获得5%左右的性能提升，原文如下

at the moment we allow libev the luxury of two heaps,
a small-code-size 2-heap one and a ~1.5kb larger 4-heap
which is more cache-efficient.
the difference is about 5% with 50000+ watchers.

PS:
本博客更新会在第一时间推送到微信公众号，欢迎大家关注。

参考文献

The Algorithm Design Manual
STL heap document
维基百科-堆