引言

Paxos算法由lamport大师提出，目标是解决分布式环境下数据一致性的问题。Paxos算法自发表以来以晦涩难懂著称，因此，其作者于2001年发表了一篇简化版的论文，Paxos Made Simple。虽然这篇论文比前面的充满公式证明的论文容易理解，但是，如果对于Paxos算法本身要解决的问题不够理解的话，还是会很难理解该算法。Paxos原理系列文章的目标是在充分讨论Paxos要解决的问题的前提下，深入地分析和理解Paxos的原理。本文是此系列文章第一篇，主要内容如下：

Paxos算法要解决的问题是什么？
Basic Paxos在整个Paxos算法中的地位及其原理

本文收录在我的github中papers项目，papers项目旨在学习和总结分布式系统相关的论文。

Paxos算法要解决的问题

首先，来描述一下Paxos要解决的问题，分布式环境下数据一致性问题。

考虑下面的环境，如下图：

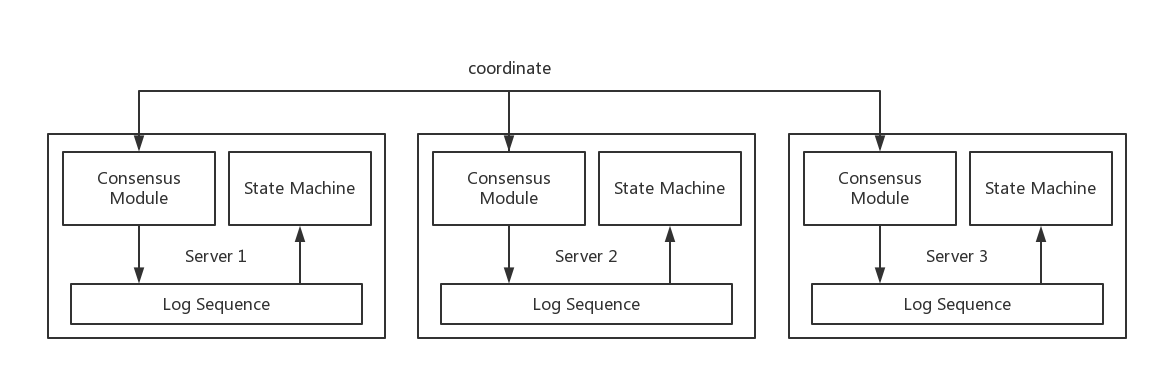
在分布式环境中，为了保证服务的高可用，需要对数据做多个副本，一般是日志的方式来实现，即图中的log sequence，当某台机器宕机后，其上的请求可以自动的转到其他的Server上，同时会新找一台机器（为了保证副本数量足够），自动地把其他活着机器的日志同步过去，然后逐步回放到State Machine中去。如果Server 1,2,3中的日志是一致的话，可以保证这些Server回放到State Machine中的数据是一致的。那么问题来了，如何保证日志的一致性呢？这正是Paxos算法解决的问题，即如图中的Consensus Module所示，它们之间需要交互，保证日志中内容是完全一致的。

进一步来看日志中的内容，如下：

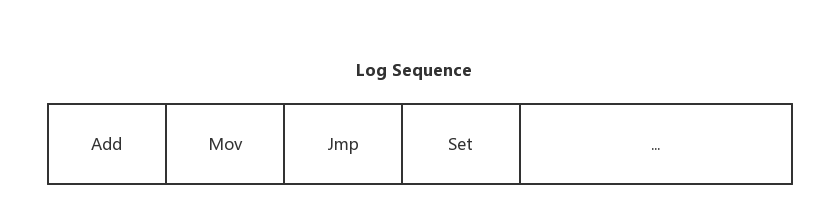
一个Log Sequence一般由多个Log Item组成，每个Log Item会包含一个Command，用于记录对应的客户端请求的命令，如图中的Add，Mov，Jmp和Set等等，每个Server会根据日志的内容和顺序，一个个的把命令回放到State Machine中。Paxos算法的目标就是为了保证每个Server上的Log Sequence中的Log Item中的Command和相对顺序完全一致，这样，在任意一台机器宕机之后，能保证可以快速地将服务切换到另外一台具有完全相同数据的Server上，从而达到高可用。

Basic Paxos

Basic Paxos要解决的问题

整个Paxos算法是为了解决整个Log Sequence一致性的问题，一般也称为Multi Paxos。而本小节要讨论的Basic Paxos是为了确定一个不变量的取值，放到上面的Log Sequence一致性上来讲，即为了确定某一个Log Item中的Command的取值，保证多个Server一旦确认该Log Item的Command之后，其值就不会再变化。

以一个例子描述确认Log Item的取值问题，如下：

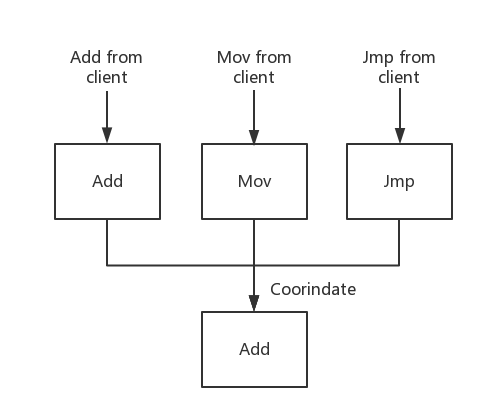
如上图所示，每个Server从客户端接受到的请求可能不一样，例如，图中的三个Server分别接收到Add，Mov和Jmp等三个不同的请求，而对于当对于当前的Log Item来讲，只能存储一个请求，而为了保证Log的一致性，又必须要Log Item中存储的Command是一致的，因此，三个Server需要协调，最终确定此Log Item存储哪一个请求，这个确定的过程就是一轮Basic Paxos过程。

最后，以比较正式的方式来定义此问题：

假设一组进程能提出（propose）value，分布式一致性算法能保证最终只有一个value被选择（chosen）。如果没有value被提出，那么就没有value被选择。如果一个value被选择了，那么这组进程能学习（learn）到被选择的value。

总体看来，一致性算法的需求如下：

被提出的value中，只有一个value被选择
进程在value被选择前，不应该能学习到该value

根据上面的问题，算法中总共有三类角色，即proposers，acceptors和learners，实际的实现中，一个进程可能承担三种角色中的一个或多个。这些角色之间通过发送消息的方式来相互通信，并且是在非拜占庭场景下：

角色的计算速度可能不同，甚至可能因为宕机而终止运行，随后又被重启。在没有记录之前已选择的value的情况下，之前选择的value会丢失，因此，需要记录之前已选择的value
消息可以时延很长，可以重复，可以丢失，但是其内容不能被篡改

在了解了上述需求，问题定义及场景后，接下来一步步地推导出Basic Paxos的最终算法。

如何解决问题？

整个问题分为两块：

如何选择value？
如何学习value？

如何选择value？

首先，来看一个最简单的方案，如下：

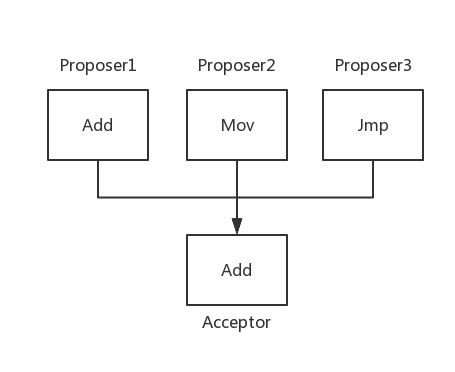
只有一个acceptor，这个acceptor只认第一个Proposer给它提出的value，例如，在上图中，如果Proposer1先把value提给acceptor，那么acceptor最终会选择该value，即Add。

此方案的优点是简单易懂，但当acceptor挂掉并无法恢复之后，被选择的value也跟着丢失了，不满足需求。

因此，接下来的方案中，只考虑多个acceptor的场景。

为了保证仅有一个value被选择，需要在多数派的Server接受该value时，才认为该value被选择。因为任意两个多数派的acceptor集合中，必然有一个acceptor是相同的。举个例子，如果不是必须多数派的话，可能出现的场景时，有前1/3的acceptor选择value1，中间1/3的acceptor选择value2，最后1/3的acceptor选择value3，这样就会导致不止一个value被选择，不符合要求。

因为消息是有可能丢失的，因此，当只有一个value被提出的时候，acceptor应该接受它，即

P1. acceptor必须要接受它接受到的第一个value

但这会导致如下问题：

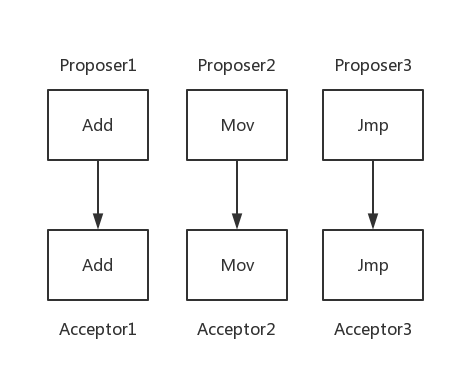
假设Proposer 1,2,3分别提出Add，Mov和Jmp，且Proposeri{i=1,2,3}首先提给Accepti{i=1,2,3}，这样会导致最终每个acceptor都接受（accept）了不同的值，最终没有value被选择。

P1和某个value只有被多数派的acceptor接受后的条件表明，每个acceptor需要能接受多个value，因此，需要通过某种方法来区分，这里采用假设每个proposer提出的value都被分配了一个id，id为自然数，每个(id,value)组合称为一个proposal（提案）。每个proposal的id都是不同的。此时，如果一个value被选择，会对应于一个或多个proposal被多数派的acceptor接受，且该proposal的value对应于被选择的value。

由于允许多个proposal被选择，因此，需要保证每个被acceptor接受的proposal的value都相同，故有如下推论

P2. 如果一个proposal(id1, v1)被选择，那么，每个id大于id1的，被接受的proposal的value都等于v

由于proposal被选择，至少需要一个acceptor接受，因此，可以由P2进一步地加强约束到

P2a. 如果一个proposal(id1, v1)被选择，那么，每个id大于id1的proposal(id,value)，如果被任意一个acceptor接受的话，value=v1

但P2a会存在如下问题：

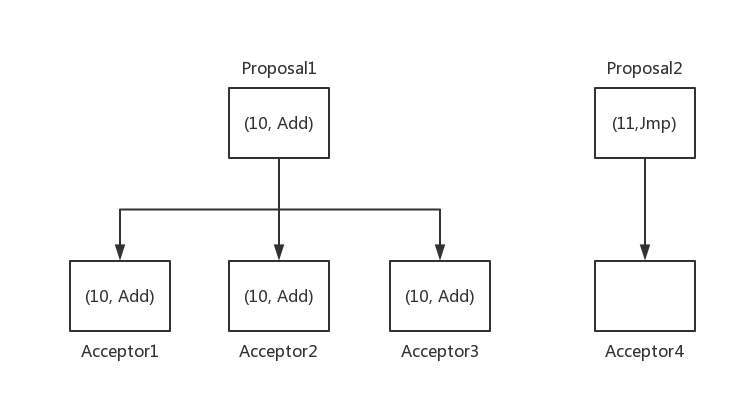
考虑以上场景，Proposal1的(10, Add)proposal被三个acceptor接受，但是，Proposer1和acceptor4之间网络不联通，导致acceptor4一致为接受任何的proposal。此时，有一个新的proposal2加入，并且能和acceptor4联通，并且，其提出的proposal为(11, Jmp)，根据P1原则，acceptor4必须要接受第一个接收到的proposal，即(11, Jmp)，导致其和P2a冲突。

因此，进一步增强P2a的约束为

P2b. 如果一个proposal(id1, v1)被选择，那么任意一个id大于id1的proposal的value等于v1

根据P2b，如果一个proposal(m,v)被选择，那么对于n>m的proposal的value也必须是v。假如当前最大的proposal的id为x-1，那么必定会存在一个多数派的acceptor组合C，使得每个acceptor接受的proposal都的id都属于[m,x-1]，且都拥有值v，并且，每个id属于[m,x-1]的proposal，如果其被任意的acceptor接受，其value必为v。

继续对P2b加强约束，由于任意的多数的集合S，至少包含C中的一个acceptor，而每个这样的集合中，id最大的proposal的value肯定是已经选择的value，因为，P2b保证了在有proposal(m,v)被选择后，其后id大于m的proposal的value肯定是v，因此，所有acceptor中只可能处于id小于m的proposal的value不等于v，所有id大于或或等于m的proposal其value必定是v。
从而，我们可以得出，任意一个proposal(x,v)，至少满足以下条件之一：

P2c. 存在多数派的acceptor集合S，对于任意的proposal(x,v)，需要满足以下条件之一：

S中的任意一个acceptor都没有接受过id小于x的proposal

S中的acceptor接受了id处于[0…x-1]的proposal，其中，v是当中id最大的proposal的value

因此，对于一个新提出的proposal，其必须要先学习到已经被或者将要被accept的id最大的value。要预测将要被accept的proposal是很困难的，但是，我们可以在acceptor中加限制，即，如果acceptor已经接受过(n,v)了，那么任何的id小于n的proposal都不会被接受，这样就能保证当前获取到的最大的id是正确的，举个例子说明：

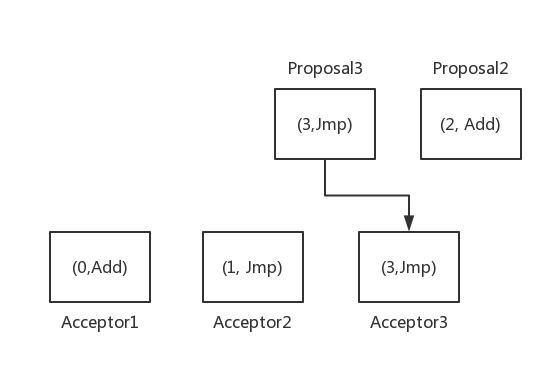
上述例子发生的场景如下：

Proposal2在Acceptor2还没有accept (1,Jmp)的时候，学习到当前最大的proposal的value是(0,Add)，因此，提出了Proposal2(2,Add)
Proposal3在Acceptor3接受了(1, Jmp)的时候，学习到当前最大id的Proposal的value是(1,Jmp)，因此，提出了Proposal3(3,Jmp)
由于网络或其他原因，Proposal3先到达Acceptor3，于是，acceptor3接受Proposal3，此时，多数派的已经达成，Jmp被选择

而后，Proposal2达到acceptor3，如果acceptor3选择接受它，那么，会出现以下情况：

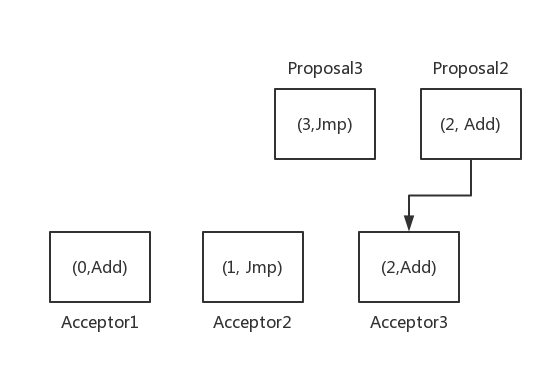
Proposal2覆盖了Acceptor3已经接受过的值，导致Add成为新的多数派而被选择，不符合要求。实际上，在Proposal3提出时，由于Proposal2并没有被接受，导致，Proposal3只能学习到(1,Jmp)，从这个角度来讲，Proposal2是属于Proposal3提出后被确认的，因此，需要在acceptor加以限制，不再接受比其接受过的proposal id小的proposal。

由上面的讨论，对于一个proposer需要经历如下两个步骤：

对于一个proposer，选择一个新的proposer id，假设为n，然后发送请求到一些acceptor组合（保证大于多数派的数量），acceptor的回应保证如下：
- 不再接受proposal id小于n的请求
- 已接受的最大的id的proposal的value

第一步称为Prepare

如果proposer接收到多数派的acceptor的回应，那么，它可以提出该proposal，id为n，value为第一步的value，或者是如果第一步的获得的value为空的话，proposer则使用自己提出的value，然后把该proposal发给一些acceptor组合（保证大于多数派的数量）。

第二步称为Accept

对于acceptor来讲，Prepare时，它都可以回应，但是，对于accept的时候，需要满足如下条件：

P1a. 一个acceptor在它没有回应一个比n大的prepare请求时，其可以接受id为n的proposal的value

值得注意的是，当一个acceptor已经回应了比n大的prepare请求时，就没必要回应小于或等于n的prepare请求了，因为后者肯定不会被accept了。因此，对于acceptor来讲，需要记录最大的prepare的proposal id，为了防止acceptor宕机后重启的情况，故最大的proposer的id需要被持久化存储。

用伪代码表达proposer的算法如下：

Prepare()
{
    select a proposal id n;
    send a prepare request with id n to a majority of acceptors
}

Accept()
{
    if get responce from majority {
        send proposal(n, v); // v is the hightest-numbered proposal's value from reponses, or if any value if the responsed reported no proposals
    } else {
        abort()
    }
}

用为代码表达acceptor的算法如下：

Prepare()
{
    if receive prepare request id with n > max_prepared_id recoreded {
        send(not accept proposal numbered less than n);
        send(highest-numbered proposal it has accepted if exist)
        max_prepared_id = id
    } else {
        do nothing;
    }
}

Accept()
{
    if max_prepared_id == request_accept_id {
        accept the proposal
    } else {
        do nothing
    }
}

如何学习value？

最简单粗暴的方案是，每当一个acceptor接受了新的proposal的时候，就广播给所有的learner，假设acceptor的数量为m，learner的数量为n，那么需要O(m*n)通信的开销。

为了减少通信开销，可以选出一个learner，负责接收acceptor的消息，然后再由它通知给其他的learner，这时需要O(m+n)。这个方法的缺点是如果这个learner宕机了，整个系统就无法正常工作了。改进的方案是，选择一组learner，假设数量为c，负责接受acceptor的消息，这些leaner负责通知其他的leaner，该方案的通信开销为c*o(m+n)，且可用性比较高，只要c个learner中没有全部宕机，系统就可以正常工作。

总结

本文分析和讨论了Paxos算法要解决的问题，即分布式系统中数据一致性的问题。为了实现数据一致性，需要保证各个副本的日志序列的一致性，而日志序列是由一个个的日志项组成的，Basic Paxos算法的目标是为了解决单个日志项的一致性。直观的来看，日志序列的一致性可以用多轮的Basic Paxos来达到，但是，往往出于性能，算法稳定性等原因的考虑，需要对多轮的Basic Paxos做优化，这就是接下来要讨论的Multi Paxos算法，敬请期待。

PS:
本博客更新会在第一时间推送到微信公众号，欢迎大家关注。

参考文献

Paxos Made Simple